Hydraulic Servo Control Using a PLC, Part 2

1. Simple proportional-only motion with a natural frequency of 10 Hz for the system.

2. Simple proportional-only motion with a natural frequency of 20 Hz for the system.

Notice that there are no acceleration and deceleration ramps. It is possible to increase the proportional gain higher than the optimal proportional gain. Doubling the proportional gain will reduce the following error, but it will not reduce the settling time. Increasing the proportional gain too much will result in overshoot or possibly continuous oscillations, which could damage the machine.

Options for Faster Response

There are a few options, but most require a target generator. A target generator calculates the target position, velocity, and acceleration every loop time. The target position moves smoothly and continuously from the current position to the command position using the command velocity and acceleration. The target generator may also generate a target velocity and acceleration every loop time. This complicates the target generator significantly. The purpose of calculating the target velocity and acceleration is to use these values to estimate the required control output to move at the target velocity and acceleration without using the proportional gain.

For instance, if the open-loop gain of the system is 10 (mm/s)/% control output, then sending a control signal of 50%, (usually 5 V on a ±10 −V output,) will result in the actuator reaching 500 mm/s. An output of 10% will result in a speed of 100 mm/s. The goal is to predict the control output for any velocity or acceleration.

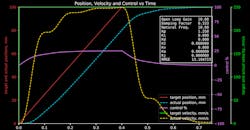
However, difficulty arises from the non-linear behavior of valves widely used in hydraulics. Even linear valves are not perfectly linear. However, output does not need to be predicted perfectly. Keeping the predicted output accurate to within 5% of the actual value will reduce the need for the proportional-only control to correct for the 5% of error. This effectively reduces the following error by a factor of 20. Therefore, the improved motion controller uses a proportional gain that is multiplied by the error between the target and actual position—but it also adds the velocity feed-forward term. It is easy to see the improvement in Fig 3. There is a little overshoot, but the response is faster. Plus, the root-mean-squared error (RMSE) between the target and actual position is much less.

3. With proportional-only gain with velocity and acceleration feed forwards, notice that the actual position and velocity lag behind the command when accelerating and overshoot the command while decelerating.

Integrator and Derivative Gains

If an integrator gain is added to the closed-loop control without using feed forwards, the integrator will “wind up” and cause overshoot while “unwinding.” Basically, the feed forwards predict what the integrator will be doing, but without the error. If the feed-forward gains are set correctly, little or no following error will occur, so the integrator will wind up little, if at all. (Monitoring the integrator is a good way to tell if the feed forward gains are set correctly! If the integrator term stays close to zero, this means the feed forward gains are predicting the control output accurately.)

4a. Proportional-Integrator control response shows the response and the overshoot due to the integrator winding up.

4b. Proportional-Integrator control windup exceeds 20%.

5a. Proportional-Integrator control with feed forwards.

5b. Proportional-Integrator control with feed forwards showing little integrator windup. The scale for this figure is much different from Fig. 4b.

Notice that the integrator does not wind up much when using feed forwards. The integrator output scales are much different between Fig. 5a and b by a factor of about 50. So the overall response is much better when using feed forwards with a PI controller. Also, the RMSE is just a little lower with proportional control and feedforwards than with proportional and integrator control with feed forwards.

A derivative gain will add bandwidth to the system. This means the actuator will respond better to higher-frequency targets. Because the derivative gain is multiplied by the error between the target and actual velocity, a target velocity must be generated. Another challenge is to compute an accurate actual velocity from the position feedback.

6. Proportional-Derivative control with feed forwards.

The proportional-derivative controller with velocity and acceleration feed forwards is just a little better than the proportional controller. However, this simulation does not reflect the difficulties of computing an accurate actual velocity due to quantized position inputs and sample jitter! PLC programmers often use a low-pass filter to remove some of the noise in the actual velocity, but this adds phase delay. In the end, a simple low-pass filter will do about as much harm as good. There are advanced ways of filtering the feedback, like Kalman filters and Observers, but these are too difficult to implement in a PLC.

 Most motion controllers use PID control plus velocity and acceleration feed forwards, with all the benefits and problems mentioned above. Actually, the derivative gain is of little benefit with under-damped hydraulic actuators, so the response of the PID plus feed forwards is about the same as just the PI plus feed-forwards controller.

The Target Generator is the Most Complicated Part of a Motion Controller

Writing the target generator is not easy. Solving for a simple point-to-point move for a trapezoidal motion profile requires solving for five unknowns using five equations.

The simplest way to start is to use linear ramps to ramp the target velocity up to the command velocity. This technique uses second order equations during ramp up and ramp down. The next step increments the target position at a constant rate until it is time to ramp down to the command position. This sounds simple enough as long as the distance traveled is long enough so the target velocity can ramp up to the command velocity and there is still enough distance to ramp down to the command position.

What if the move is a short move? Then the command velocity will never be reached. The programmer will find there are a lot of “what-ifs.” What if the command position and velocity is changed during the move? The math becomes more complex and it will take a long time to debug. Writing target generators should only be attempted for simple cases where the command position, velocity, and acceleration are not changed during the move and there is enough distance so the target velocity will reach the command velocity.

Commercial motion controllers use a series of third order or higher polynomials. A simple move may require solving 17 equations with seventeen unknowns. This is far beyond what one would want to solve using a PLC.

No Target Generator Required

There is an option that doesn’t use a target generator and still keeps the integrator from winding up, but this requires writing your own closed loop control. This option uses an integrator and proportional gain, with the derivative gain being optional. What makes this method different is that the proportional gain is not multiplied by the error between the target and actual position, but is multiplied by the change in the actual position, and is added to the last control output just like the integrator term would be. The error is calculated as the difference between the command position and the actual position, but this value may be large, so the error is limited by the maximum error. The integrator gain is multiplied by the minimum value of the error between the command and actual position and the maximum error. The programmer can control the system’s speed by setting the value of the maximum error. As the actual position approaches the command position the error between the two will decrease and the actuator will slow down to a smooth stop if the values for the integrator and proportional gain are chosen correctly.

Figure 7 is an example of a 500 mm move with the maximum error set so that the maximum speed should be about 250 mm/s. The slight velocity overshoot at the beginning can be reduced by adding a derivative gain to smooth the acceleration.

7. The proportional gain is multiplied by the difference between actual position and the previous actual position, then added to the control output.

This approach is not that fast, but it will provide a relatively smooth motion no matter how far the actuator must move. The optimal response is determined by the natural frequency and the damping factor.

Clearly, there is a lot to consider when attempting even a simple point to point hydraulic servo control in a PLC or a small micro controller like an Arduino. It takes time to write the necessary algorithms and this is made more difficult if the only language available is ladder logic. Is there more that can be done to improve performance? Yes! However, the control theory for hydraulic actuators is not covered well or at all in textbooks, so there is little to guide a person writing a commercial quality hydraulic servo controller from the bottom up. Commercial motion controllers use complex algorithms that would take too long to write and debug, unless it can be justified by volume.

A future article will present a few examples of controlling a hydraulic cylinder with a PLC.

Peter Nachtwey is president of Delta Computer Systems Inc. and has more than 35 years of experience developing industrial control systems for hydraulic, electric, and pneumatic applications. In addition to leading Delta’s engineering and R&D programs, he contributes widely to the mathematical understanding of control theory, especially in fluid power systems.