Speed Control of Hydraulic Motors

Figure 1. Valve control of motor speed uses a constant pressure source; a closed center 4-way proportional/servo valve; the motor to be controlled, which propels a load torque at some speed; and an amplifier to supply controllable current. Click on image for larger view.

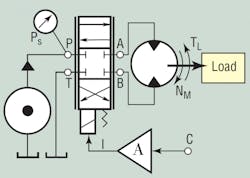
A typical valve-controlled system is shown schematically in Figure 1. The design of the speed control system consists of two parts. The first is optimal sizing of components so that maximum power is transferred to the load at the design point. The second is a feedback control method configured to provide a wide enough speed range and degree of speed control to maintain constant speed of a changing load.

Consider an application, such as a conveyor drive, where the load varies at any given moment, and the speed must be adjustable or synchronized with some other process action. The design point is the single, worst-case operating point where the power required by the load is greatest. It consists of the load torque requirement at the design point, T_L,DP, and the speed required at that torque, N_M,DP.

Because this is the worst-case point, if we design to that point, all other operating conditions will be within the operating envelope of the hydraulic system — we will have stacked the odds in favor of a successful application.

Optimal sizing, also called optimal design, involves evaluating and selecting the three key hydraulic parameters: supply pressure, P_S, valve coefficient, K_V,T, and motor displacement, D_M, such that maximum power is transferred to the load at the worst-case design point.

Optimal sizing

When optimizing a design for a hydraulic motor application, mathematically speaking, we can create two equations, but there are three hydraulic parameters to be evaluated — supply pressure, motor displacement, and the valve coefficient. Therefore, one of the three has to be known, or specified, after which the other two can be calculated.

A complete development would have to be done to cover all three situations, one for each of the three possible known quantities at the outset. For the development at hand, we will be using only one of the three possibilities: that is, the situation where the supply pressure is specified, and therefore we need to calculate the displacement and valve coefficient.

Figure 2. To facilitate analysis, the Analytical Schematic of the valve identifies all four ports and the two active valve lands, powered and return. Click on image for larger view.

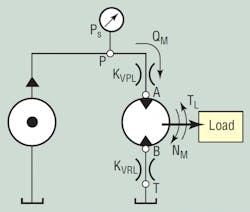
The orifices in Figure 2 represent the powered and return lands of the servo or proportional valve. These orifices often are called the meter-in and meter-out land, respectively. However, in this text, the more modern notation will be used. The motor and constant pressure pump are represented in a conventional way.

Of course, the supply pressure must equal the sum of the differential pressure losses for the valve lands and the motor. Figure 2 helps illustrate the various pressure drops. From a knowledge of hydraulic circuit analysis, it is further known that the valve pressure losses relate to the square of the flow through each respective valve coefficient.

Without getting into the mathematical derivation, this leads to the Valve Control of Motor Motion (VCMM) equation.

This equation expresses the relationships between supply pressure, valve coefficient, motor displacement, plus the two load variables, load torque, and load speed. At design time, we must have a knowledge of the load torque and shaft speed requirements. With the VCMM Equation, we solve for the motor displacement and at the same time impose the condition for optimality; that is, the stall torque.

Stall torque must be 1½ times the running torque at the design point. Of course, at stall, flow through the motor is only leakage.

Motor displacement can be calculated. However, there is a dilemma that often exists in hydraulic circuit design. Specifically, we need to know the mechanical efficiency of a motor as well as its leakage flow even before we know anything about the motor! Fortunately, if we have some experience with hydraulic motors, we can guess at reasonable values for the motor's mechanical efficiency and flow leakage, both under stall conditions.

A reasonable approximation is that the expected torque (mechanical) efficiency at stall will be 75 to 95% for most motors.

Determining flow leakage is more complicated. It is the leakage flow through the motor when full supply pressure is applied to the valve inlet port and the motor has so much load on the shaft that it cannot turn. Clearly, the only flow will be that which leaks through the motor's internal clearances. The value will be small compared to the flow at full speed.

Referring to Figure 1, imagine we apply so large a load to the shaft that it is brought to a halt, even though full pressure is applied and the valve is fully open. Motor flow would consist only of that which can squeeze by the small, stationary internal clearances. Now consider the amount of pressure drop across the fully opened valve with such a small flow. It will be especially small, if the motor has a reasonably high volumetric efficiency. When the maximum volumetric efficiency is between 80 and 95%, the valve pressure drop at stall will be about 3 to 10% of the applied supply pressure.

With these approximations, plus some engineering sense, we can calculate a fairly good estimate of the required motor displacement. Most likely, the exact calculated displacement will not be commercially available. Therefore, we will have to select the nearest displacement, along with the pressure, speed, and torque requirements, and assess the motor's suitability for the application.

The VCMM equation can be evaluated at the worst-case design point, then used to solve for the required valve coefficient. Clearly, the speed and torque values must reflect the worst-case design point, but so too, do the volumetric and mechanical efficiencies of the motor.

Note that the efficiencies at the full load operating point may be quite different from the efficiencies at stall. Inexperienced designers may estimate volumetric and mechanical efficiencies to fall between 75 and 95% for most motors. However, experienced designers should use values that they feel comfortable with.

There are many other observations, but their assessments will be left to the interested reader. An example problem will be introduced next month to help reveal other meaningful observations.