Hydraulic-Electric Analogies — Part 6: Coils, Cores, and Transformers
Lenz’s Law explains more than just the “speed voltage,” which also happens to be another moniker for that law. It says an induced voltage will occur anytime there’s relative motion between the conductor and the magnetic field. Therefore, the conductor can move relative to the field, or the conductor could be stationary while the magnets move, or they could both be in motion. All will result in an induced voltage in the conductor. They just require relative motion between the conductor and the field and a transverse component to the relative motions. That is, if the conductor followed along a flux line, there would be no induced voltage. A complete closed electrical path also produces an induced current in the conductor.
The scenario of interest here is when both magnets and conductors are stationary, yet the current is changing to prompt a change in the magnetic field. Again, a voltage will be induced; change only occurs to the current and magnetic field.
When the flow path is a coil, the flux lines from one loop combine with flux lines in adjacent loops to increase magnetic field strength. When there’s only one set of loops (i.e., only one coil), the circuit element is called an inductor. The core may or may not be iron; Figure 8 shows the schematic symbols for air and iron-core inductors.
The electrical property of a coil, called its “inductance,” is measured in henries (abbreviated as “H,” or sometimes “h”). The working units of inductance are volt-seconds/ampere, which adds an element of time. The algebraic and schematic diagram identifier for an inductor is an unlikely L. An iron core in the coil results in tens or even hundreds of times greater inductance than an air core for the same number of coil turns and current.
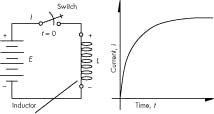
Lenz’s law also says that the induced voltage’s polarity will oppose the change in current that caused it. Thus, the induced voltage will “delay” the current build up, like when a switch is closed in a battery-inductor circuit. A circuit that shows a battery being used to energize (electrically excite) an inductor, L, at the moment the switch is closed (t = 0), coil current is zero but rising (Figure 9).
Inductance relates to current and voltage as force and velocity relates to a physical mass. If a force is applied to a mass, velocity of the mass gradually increases because it’s impossible to have infinite acceleration. Inductance is a form of electrical mass or inertia. It would take infinite voltage for the current to change instantaneously. And it would take infinite force to get a finite mass’s velocity to change instantaneously.
Electrical energization tries to increase the current. However, the induced voltage caused by the changing current has the polarity shown in Figure 9 (+ on top and – on the bottom) and “shoves back” against the battery voltage. Therefore, the current at the first instant is 0.
Still, the changing current eventually results in a current buildup, which can be seen in the graph on the right (Figure 9, again). This “exponential rise in current” is caused by the inductor’s time-effective properties. Eventually, the current will reach a plateau (the time can be on the order of nanoseconds for very small inductance, or on the order of seconds with a very large inductor). Both the battery voltage and the parasitic resistance of the coil determine the current plateau (not shown in the figure).
The time required for the current to reach its plateau, also called the “steady-state” value, is given approximately by 5 L/R, where L = inductance in henries, and R = parasitic coil resistance in ohms. The L/R ratio is the coil’s “time constant”; its units are simply seconds. The general rule is that it takes five time constants to reach steady state.
One important factor to remember: Inductance puts time-dependence into electrical events. As stated earlier, a “delay” occurs in the buildup of current. In other words, rather than jump up immediately to the steady-state value, it takes time. We say that “inductors oppose changes in current,” i.e., the current cannot change instantaneously. Voltage can, but current cannot.
Transformers
Now that we know a single coil can induce a voltage in itself, what if two coils are near one another? Will one induce a voltage in the other? The answer is, most emphatically, yes! In fact, fluxes of two electrical coils that link to one another is an exact representation of a transformer.
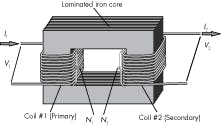
A real transformer is hardly more complicated than the simple, two-winding transformer shown in Figure 10. The “primary” winding has power applied to it, while electrical power taken from the “secondary” winding supplies some load. As long as the power ratings aren’t exceeded, most primaries and secondaries can be switched without undue consequences. The device is more or less bidirectional in terms of energy flow direction.
How does a transformer work? Foremost, transformers will ONLY work with alternating voltage — not direct current. Also, the flux must be changing; applying ac to the primary winding ensures flux change. A laminated iron core enhances flux buildup and magnetic intensity. Because the iron core is common to both windings, the primary’s flux links with the secondary winding. The ac power ensures that the flux varies with time. As a consequence, a voltage is induced into the secondary winding with no electrical connection other than the mystical magnetic flux.
The physics of Lenz’s Law demonstrate that the secondary (output) voltage’s amplitude is the relative number of turns of the primary winding to the secondary winding. For the ideal transformer, the output power is equal to the input power:
V1 × I1 = V2 × I2 (1)
Manipulating the equation slightly and introducing the turns, voltage, and current ratios results in:
V2 ÷ V1 = I1 ÷ I2 = N2 ÷ N1 (2)
This last equation expresses that if more windings are in the secondary coil (N2), the secondary voltage (V2) will be greater than the primary excitation voltage (V1). This is called a “step-up” transformer because it raises the voltage. Obviously, fewer turns on the secondary will result in a “step-down” transformer.
Equation 2 also reveals that a boost in voltage must result in reduced current. Suppose the load on the secondary increases, meaning the load needs more current. The primary current must likewise increase, because the primary’s volt-ampere product (input power) must be equal to the secondary’s volt-ampere product (output power), internal losses notwithstanding. This is, at once, a description of the transformer (Equation 2) as well as a statement of energy conservation (Equation 1).
Core lamination
One may question “Why is the core laminated?” Lenz once again provides the answer. As already stated, the core must consist of materials, mostly ferromagnetic, with flux-enhancing properties. But those materials are also electrical conductors that may have induced voltages and currents. The same is true of the core: Alternating flux in the core material induces internally circulating currents, called “eddy currents,” that generate heat in the resistance of the core material.
As shown in Figure 11, when the cores are laminated with the desired ferromagnetic material and the laminations are separated electrically from one another by a thin coating of electrically insulating varnish, it reduces the net magnitudes of the induced currents. This keeps the core cooler and improves the transformer’s efficiency.
Currents are induced in a transverse direction from the inducing flux lines. Meanwhile, the laminations, when arranged as suggested in Figure 10, don’t significantly impede the flux, but will impede the currents. Therefore, current in the laminations is forced to take long narrow paths. All magnetic devices operating on alternating current feature laminated cores.
Laminations are always aligned with the flux lines to the extent where losses can reach their lowest levels. For example, dc solenoids inadvertently operating on ac can quickly burn up due to excessive eddy currents in the unlaminated core.