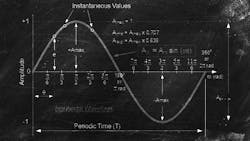
Many test systems use sine wave (sinusoidal) motion. Sinusoidal motion profiles are easy to generate because most computers and PLCs have sin functions either built in or as an additional library. However, generating the motion profile is not the hard part.
Basics
Too many times we have seen failed systems or been asked ridiculous questions because the designers didn’t fully realize the challenges of making sinusoidal systems. They usually look at the basic definition, which is:
position(t) = amplitude ⋅ sin(2π ⋅ Hz ⋅ t)
The frequency in Hertz (Hz) must be multiplied by 2π to convert Hz to radians per second for the sine function. This is easy enough.
The velocity should be calculated as well so the hydraulic designers can ensure the actuator will move fast enough. The velocity is easy to calculate using the definition of the derivative of a sine function
velocity(t) = amplitude ⋅ cos(2π ⋅ Hz ⋅ t) ⋅ 2π ⋅ Hz
The velocity as function of time should also be calculated for velocity feed forward (VFF) calculations.
The peak value of a sine or cosine function is 1, so it is easy to calculate peak velocity:
peak velocity = amplitude ⋅ 2π ⋅ Hz
The next step usually gets people into trouble. The acceleration is the derivative of the velocity:
acceleration = amplitude ⋅ − (sin2π ⋅ Hz ⋅ t) ⋅ (2π ⋅ Hz)2
The acceleration should be calculated so acceleration feed forwards (AFF) can be calculated, but the ‘gotcha’ is the peak acceleration.
Peak acceleration is:
peak acceleration = amplitude ⋅ (2π⋅Hz)2
Notice that the peak acceleration goes up with the frequency squared. This means a sine wave of 20 Hz has a peak acceleration four times that of a sinewave at 10 Hz. That means the system’s natural frequency must be four times higher and the valve must have a frequency response four times higher.
The Frequency Problem
A distributor once asked if we could control a sinusoidal motion with an amplitude of 5mm (0.005m) and a frequency of 75 Hz. My usual response is “Sure, we are only moving electrons.” Anytime I hear a request to for sinusoidal motion at frequencies over 10 Hz, I know the project will not be easy. My counter question is “Can you design a hydraulic system that can deliver accelerations this high?” In this case the peak velocity and acceleration would be:
peak velocity = 0.005 ⋅ (2π ⋅ Hz) = 2.356 m/s, or almost 93 in/s
To accelerate to this speed in a space of 5 mm then slow to 0 m/s in 5 mm would be challenging.
peak acceleration = 0.005 ⋅ (2π ⋅ Hz)2 = 1110 m/s2 = 113g
A one-pound mass needs one pound of force to accelerate at 1g. Clearly it would take an expensive system to accelerate anything at 113g, if it could be achieved at all. I knew this was not going to happen because big hydraulic valves that move that much oil are usually not fast enough. Even if the amplitude was reduced to 1 mm (0.001m), the peak acceleration would still be 222m/s2 or 22.6g.
Typical accelerations in industrial applications are about one quarter g. Typical values are 100 inches per second-squared when using imperial units and 2,500 millimeters per second-squared when using metric units. So, accelerating to 1,110m/s2 is too much. Obviously, the project was abandoned. My contribution was keeping the end customer from making a costly mistake.
Other Approaches to Control
Servo valves should have frequency responses three to four times the desired frequency; otherwise the valve’s response will start to slow the response of the sinusoidal motion in addition to the rest of the system, causing it to lag even more. The velocity, acceleration and even jerk feed forwards can compensate for the frequency of the actuator and load, but not the valve.
If the valves’ frequency response is not high relative to the desired frequency, then closed-loop control will not work very well. It will be impossible for the controller to keep the error between the target and actual positions, velocities and accelerations within acceptable limits. In this case, adaptive control is required.
Adaptive sinusoidal motion does not try to keep the error between the target and actual positions small. Instead, it is a semi-open-loop mode where the open-loop signal is adjusted so the peak of the actual position will be the same as the desired peak, but there will be a phase lag between the actual position and target position.
One problem that will occur is that a single-rod actuator will tend to extend because the open-loop gain is higher in the extend direction than in the retract direction. This means the open-loop sine wave must also have the amplitude of the outputs scaled so the actuator doesn’t slowly extend further and further during the test. The effect can be greatly reduced if double-rodded cylinders are used, because the area of the piston is the same on both sides (assuming the rods are the same diameter).
Supplying the Power
Pumps are also often sized incorrectly. Most of the time, the required pump size is overestimated because peak flow is used instead of average flow. Average flow is about 0.64 of the peak flow. If the accumulator is sized correctly, the pump can be safely sized to supply about 0.7 of the peak-flow values. Sizing the pump using peak flow will still work but will result in a larger pump than necessary.
The HPU should be sized for the average flow, plus a little more for a safety margin and also to take into account that some of the oil does not actually move the actuator directly; it is used to compress the oil to increase force to accelerate the load. An accumulator or two should be used to supply the peak oil flow and to rely on when the velocity of the sine wave is slow to recharge the accumulator. HPUs cannot respond to the flow demands of a sine wave fast enough, so accumulators are needed to supply oil when the pump cannot.
Another problem is choosing the correct type of pump. Pressure-compensated pumps are a common choice, but the pressure compensation cannot keep up with the system’s flow and pressure fluctuations. Also, the swash plate ends up cycling back and forth over a small range, which tends to wear out the pump in that range of swash plate motion. A better solution would be to use a fixed-displacement pump powered by a variable-speed motor.
The motion controller would know how much oil is being used at any time based on the amplitude, frequency of the motion and piston area. The flow calculation can be used as a feed forward for predicting flow. The motion controller can then change the motor’s speed as necessary, but still run at a relatively constant speed, relying on the accumulator to keep the pressure somewhat constant. There would be a small amount of error in predicting flow, so there still needs to be a pressure sensor to ensure the pressure stays in the desired range.
Peter Nachtwey is president of Delta Computer Systems Inc.
About the Author
Peter Nachtwey
President,
Peter Nachtwey has more than 35 years of experience developing industrial control systems for hydraulic, electric, and pneumatic applications. He graduated from Oregon State University in 1975 with a BSEE and served as an officer in the U.S. Navy until 1980. He became president of Delta Computer Systems Inc. in 1992. In addition to leading Delta’s engineering and R&D programs, he contributes widely to the mathematical understanding of control theory, especially in fluid power systems. He has also presented technical papers for IFPE, NFPA, FPDA, and various global technical conferences.

Leaders relevant to this article: