The geometric approach to building motion profiles
By Jack L. Johnson, P.
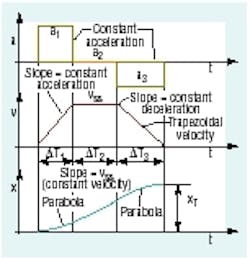
Figure 1. Constant acceleration profile (top) and resulting velocity (middle) and position (bottom) profiles are interdepedendant upon each other.
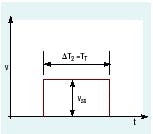
Figure 2. Rectangular velocity profile gives minimum requirement of maximum velocity.
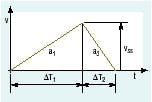
Figure 3. Triangular velocity wave shape minimizes acceleration but maximizes maximum velocity.
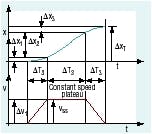
Figure 4. Acceleration change points are given in terms of time and actuator position.
The geometric approach to profile synthesis and analysis is a more intuitive method than the analytical approach covered last month. The geometric approach capitalizes on the fact that an integral is the area under a curve and a derivative is the slope of a curve. It still requires some mathematical manipulation, but it is all algebra. When we limit the discussion to constant acceleration motion, as depicted in Figure 2, the problem becomes quite manageable.
Scenario #1: Total cycle time, total distance and time change intervals are specified — In this scenario, which occurs frequently in industrial applications, the velocity wave shape is fairly well specified. However, we don't know the maximum velocity, Vss. We can find it by knowing that the position is the area under the velocity curve. With constant acceleration, the total distance is the area under a triangle, plus a rectangular area plus another triangular area, Figure 2. That is:
XT= 1/2VssΔT1 + VssΔ T2+ 1/2VssΔT3
The only unknown quantity is maximum velocity, Vss. It can be solved for:
Vss = XT ÷ (1/2îT1 + î T2+ 1/2îT3)
To put this into practice, consider it necessary to extend a hydraulic cylinder 43.6 in. within 2.15 sec. The acceleration time is projected to be 300 msec, and controlled deceleration will take 450 msec. What is the maximum speed?
We can calculate the second time interval from the given information:
ΔT2 = TT-ΔT1-T3 = 1.4 sec
Substituting this value and the tie intervals given allows solving for maximum speed (which is the same as the speed at the steadystate plateau):
Vss = 43.6 [1/2(0.3)+1.40+ 1/2(0.45)]
= 24.56 in./sec
Scenario #2: Only total time and distance are specified — Many times the individual time intervals are not given. Instead, they are left to the discretion of the motion control system designer. This burdens the designer with decision making, but it also gives the designer more flexibility. Let us now assume that only total time and distance are given, and that the acceleration, steady-state (maximum) velocity, and deceleration time intervals need to be determined.
No single solution exists to this problem. Mathematically speaking, an infinite number of T combinations will meet a total time and total distance specification. We can only explore the trade-offs associated with various T combinations.
So what if we use a velocity wave shape that has vertical rises and falls, as shown in Figure 2? We know that there is only one time interval, ΔT2, because the acceleration-time, ΔT1, and deceleration time, ΔT3, are zero. Therefore:
ΔT2 = ΔTT and Vss = XT÷ TT
This velocity wave shape has serious limitations. First, the vertical sides constitute infinite acceleration, which is impossible to achieve. Second, the pressure spikes are high and create shock, vibration, and noise, which reduce component life, and increase maintenance costs. Third, it can hardly be called motion control. In fact, the wave shape shown is one that is representative of on-off, not proportional or servo control.
Nonetheless, the wave does represent a limit of operation, and it allows the total distance and total time to be met with at the lowest possible maximum speed. The maximum speed (Vss) is what determines the size of the valve, actuator, and power unit. Minimizing it is a useful accomplishment. However, the wave shape of Figure 2 has minimized speed to a level that is impossible to accomplish.
Next, we assume that the acceleration will be minimized. Doing so will reduce shock and vibration. Minimum acceleration will occur if there is no steady-state velocity plateau, Figure 3.
In this case, ΔT2 is zero, giving only acceleration and deceleration times, ΔT1 and ΔT3. If ΔT1 and ΔT3 are not equal, a1 and a3 cannot have equal magnitudes. This would not constitute minimum acceleration. Therefore:
ΔT1 = ΔT3
Substituting this value into the initial equation on the previous page yields:
VSS = 2XT TT
Note that this velocity is exactly twice what is required of the rectangular velocity wave shape. Thus, the minimum acceleration situation maximizes the peak velocity and increases the valve flow rating requirement. This may or may not be a prohibitive factor; the triangular velocity wave shape is practical and sometimes is implemented. Just be aware that it demandsthe largest possible valve.
For that reason, the more typical profile is the trapezoid with a VSSplateau. It is necessary, however, to select ΔT1 and ΔT3 to prevent acceleration from inducing noise and shock. Note, further, that if the acceleration is to be minimized, then it is necessary to make ΔT1 and ΔT3 equal to each other. To do otherwise would make one — the magnitude of either the acceleration or the deceleration — greater than the other. They are minimized when they are equal.
Scenario #3: Total cycle time and ΔX intervals are specified — Acceleration sometimes must be changed at specified distances and times. For example, the profile specification may be:
- accelerate until reaching a position of 2 in.
- continue at constant velocity for 10 in. more
- decelerate to stop at the 15-in. position
- complete the cycle in 1.3 sec.
In this case, we know the transition points — often called profile corner points — in terms of specific distances. We do not know the time values, Tx, nor do we know maximum speed, VSS. We are given total time, so we can calculate the missing items.
Scenario #4: Total cycle time, total distance and accelerations are specified — Sometimes acceleration must be constrained. Moving a ladle of molten metal (or any liquid) horizontally is an example of a system with acceleration and deceleration limits. If the ladle is accelerated too fast, liquid can slop over the edges. If it is too slow, production suffers.
In this scenario, the total time, TT, is specified, along with the total distance that must be covered and maximum acceleration and deceleration. The maximum velocity required (VSS) and the individual time values (ΔTX are not specified, but can be calculated if all three accelerations are known.
Generalized profiles are shown in Figure 1 and Figure 4, and we'll assume the acceleration in the ΔT2 interval to be zero, as suggested by the graphs; the velocity at the end of the interval is also zero.
The solution will require writing two equations, the first for total distance and the second for total time, TT. Then with the constant acceleration relationships in the intervals, the total time and total distance equations can be solved simultaneously for VSS.
We begin with the expression for total distance in terms of incremental values:
XT= 1/2VssΔT1 + VssΔ T2+ 1/2VssΔT3
For constant accelerations in the two end intervals:
Vss=a1ΔT1
ΔT1 = VSS÷ a1
VSS = a3ΔT3
ΔT3 = VSS ÷ a3
Substituting these values into the equation eliminates ΔT1 and ΔT2 :
XT=(1/2V2SS a1)+VSSΔT2+(1/2V2SS a3)
Two variables remain unknown: ΔT2 and VSS. Writing an equation for the total time will produce two equations with two unknowns:
TT= ΔT1 + ΔT2 + ΔT3
TT= (VSS÷a1) + ΔT2 +(VSS÷a3)
Multiplying this result by VSS and adding it to the above equation causes the ΔT2 term to disappear. Setting it equal to zero yields:
XT VSSTT+ (V2SS÷2)[(1÷a1)+(1÷a3)]=0
This is a quadratic equation, which can be solved using the quadratic formula. We'll forgo that complicated math, but realize that only positive, real values for Vss will be meaningful. Therefore the following inequality must be satisfied:
T2T > 2[(1÷a1) + (1÷a3)]XT
We cannot indiscriminately pick values for the total distance, acceleration, deceleration, and total time. Doing so could produce an imaginary value for maximum velocity. In that case, no real, physically realizable solution to the problem would exist because the specifications would be impossible to achieve. Many possibilities and consequences can be explored.
Other Scenarios — Profiles can be specified other ways that offer real solutions. However, they are so numerous that they cannot be covered here. Perhaps it is more important to realize that you can very easy make a profile specification that is not achievable. The possibility of an imaginary value for maximum speed is but one example.
There are examples, and here are the more obvious ones:
- time calculates to a negative, or imaginary value.
- simple conflicting requirements. For example, three intervals of 1, 2, and 1.5 sec may need to coincide with total time not to exceed 4 sec.
- motion of 35 in. must occur in 2 sec, but speed may not exceed 12 in./sec.
Next month's edition of "Motion Control" will begin a study of flow profiles. Knowledge of a tightly controlled velocity profile leads to a clear vision of the flow profile. The designer need only take into account the appropriate valve port and the cylinder area controlling the flow. Pump-and tank-port flow is always unidirectional, but work-port flow is always alternating.