How Natural Frequency Limits Frequency of Acceleration
A hydraulic cylinder can be simply modeled as a mass between two springs. Systems with a low natural frequency (the frequency at which the system oscillates after a sudden start or stop) have a low spring constant relative to the mass of the load. Conversely, systems exhibiting a high natural frequency have a high spring constant relative to the load mass. So how high should the natural frequency of the cylinder be relative to the frequency of acceleration? Ideally, the natural frequency should be at least four times the required frequency of acceleration —the frequency at which the cylinder’s piston and load accelerate. This is true when using a standard hydraulic motion controller.
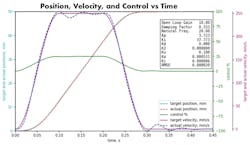
1. In this plot, the frequency of acceleration is 5 Hz and the natural frequency of the system is 10 Hz. The actual position and velocity values do not accurately follow the target values; note the Root Mean Squared Error (RMSE). The motion will be “jerky.”
Natural Frequency and Frequency of Acceleration
In a hydraulic system, the natural frequency is calculated from the mass of the load, the areas of both the rod- and cap-end of the piston, and the bulk modulus of the hydraulic fluid.
Where:
ωn is the natural frequency of the cylinder and load;
β is the bulk modulus of oil;
A is the average area of the piston;
V is the total volume of oil trapped between the valve and the piston; and
M is the mass of the load
A simple example illustrating frequency of acceleration is a cylinder and load following a sinusoidal motion at 5 Hz. In this case, the frequency of acceleration is 5 Hz. If the cylinder is just making a simple move from one position to another, the frequency acceleration is 0.5 seconds divided by the minimum of the acceleration or deceleration time. This assumes the acceleration and deceleration ramps are sinusoidal S-curves having one fundamental frequency with no harmonics. (Linear ramps have the fundamental frequency and many harmonics that may cause problems.)
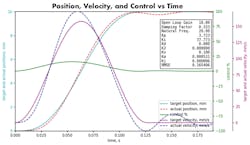
2. The same system as shown in Fig. 1, but with the natural frequency increased from 10 to 20 so that it is 4 times the frequency of acceleration. Now the actual motion more accurately follows the target motion profile. Note the RMSE value in this plot.
Most motion controllers express the acceleration as a rate. For instance, 2,500 mm/sec2 is about one fourth the acceleration due to gravity. The acceleration time to 250 mm/sec takes 0.1 second at 2,500 mm/sec2, so the frequency of acceleration is 5 Hz (0.5/0.1 sec. = 5 Hz). If the acceleration is to 100 mm/sec. the acceleration time is 0.04 sec., so the frequency of acceleration is 12.5 Hz.
I have been asked many times why the tuning for short moves needs to be different from that for long moves. The reason is that short moves have very short acceleration times; consequently, the frequency of acceleration is higher. If the natural frequency is not at least four times that of the maximum frequency of acceleration, the system will not control well.
In the example above, the 12.5 Hz frequency of acceleration may be greater than 1/4 the natural frequency. Therefore, for good control with a typical motion controller, it may be better to slow the acceleration ramp down to 1,000 mm/se.c2 so the acceleration time is still 0.1 sec.
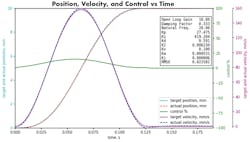
3. In this system, the frequency of acceleration is 8, but the natural frequency is only 20. Without advanced control, the following error is large.
Why Does Natural Frequency Need to be Four Times the Frequency of Acceleration?
The natural frequency does not actually “need” to be four times the frequency of acceleration. If it isn’t, you’ll find it difficult or even impossible to optimize the controller gains so the actual position follows the target position with little error. If the natural frequency is much greater than the frequency of acceleration, the controller gains will be much easier to optimize.
Here’s a graphical example: In Fig. 1, the frequency of acceleration is 5 Hz, and the natural frequency is 10 Hz. The natural frequency is only two times the frequency of acceleration, so the following error is large. (Note the root mean squared error value, RMSE.) Figure 2 shows that increasing the natural frequency to 20 Hz reduces the error between the target and actual position.
This analysis assumes the controller is capable of proportional and integral (PI) control with both velocity and acceleration feedforwards (feedforwards predict the needed control output rather than waiting for the control output to be generated by errors). If the controller is not capable of PI control, or does not support velocity and acceleration feedforwards, the ratio of natural frequency to frequency of acceleration needs to be much higher to keep the following error small.
For instance, a controller with proportional only control will still have 30 deg. of following error even if the natural frequency is 10 times greater than the frequency of acceleration. Do not use proportional-only control if the following error must be close to zero.
The most advanced motion controllers can keep the error between the target position and actual position small even if the natural frequency is only two times the frequency of acceleration.
4. With an advanced motion controller with second derivative gain and jerk feed forward, it’s possible to achieve precise control even when the natural frequency is not 4 times the frequency of acceleration. Note the reduction in the RMSE value from Fig. 3.
What Does This Mean?
Saving money! As a general rule, systems with lower natural frequency can use smaller components (cylinders, pumps, etc.), which cost less. The key is selecting the right motion controller.
Advanced electrohydraulic motion controllers can perform well when the ratio of the natural frequency to frequency of acceleration is less than four. Advanced motion controllers, such as the RMC motion controller family from Delta Computer Systems, have control algorithms beyond basic PID gain and velocity and acceleration feed forwards.
The diameter of the cylinder is roughly proportional to the natural frequency. If the motion controller allows the natural frequency to be only two times the frequency of acceleration, the cylinder diameter may be reduced up to half. How much less depends on the VCCM equation. Reducing the hydraulic cylinder diameter by half means the pump, valve, piping, and accumulator sizes can all be reduced. The cost savings can be much more than the total cost of the hydraulic motion controller. Plus, the machine will be much more economical to operate.
Figures 3 and 4 demonstrate the benefits of an advanced controller. The first plot (Fig. 3), shows a short-distance move of a system where the natural frequency is 20 and the acceleration and deceleration take only 0.125 sec. Therefore, the frequency of acceleration is 8 Hz. The actual motion doesn’t follow the target because the natural frequency is only 2.5 times the frequency of acceleration. The last plot (Fig. 4) assumes the same conditions, but with control by an advanced motion controller. The following error is very small.
Peter Nachtwey is president of Delta Computer Systems Inc., Battle Ground, Wash.
