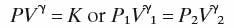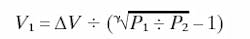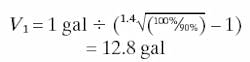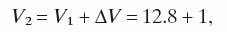Accumulators: The unsung heroes of hydraulic motion control
This file type includes high resolution graphics and schematics when applicable.
One of the most important, but possibly least understood components of a hydraulic motion system is not an active component at all. It is component that saves power, makes the system easier to control, and can extend a machine's useful life — the accumulator.
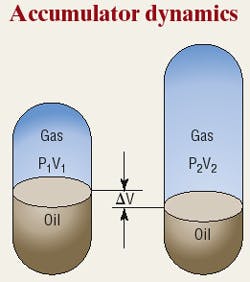
For the purpose of this article we will describe an accumulator consisting of a high-strength tank with a bladder inside and ports for the tank oil and bladder gas, Figure 1. Pressurized nitrogen gas is typically used to expand the oil when under normal operating pressure. If pressure on the oil side drops, the pressurized bladder pushes oil out of the accumulator. When oil pressure increases, then oil flows into the accumulator and compresses the bladder.
Accumulators store energy
Hydraulic systems can have a big advantage over servo motors in systems with varying loads. Although each electric actuator motor in an electromechanical system must be sized for its peak load, a hydraulic power unit (motor and pump) in an electrohydraulic system can be sized for the average power required of all of the hydraulic actuators over a machine cycle. To take advantage of this power averaging, accumulators are used to store energy when the energy demands are less than average and transmit energy back into the system to satisfy peak demands. The accumulator capacity must be high enough so the pump need not respond to quick changes in the demand for oil.
Keeping supply pressure constant
An ideal power unit would be able to supply an infinite amount of oil without allowing supply pressure to drop. Keeping the supply pressure constant is important because it keeps the gain of the hydraulic system constant. The hydraulic system gain determines how fast the hydraulic actuator moves when a control valve fully opens.
Once a hydraulic system is designed, the system pressure and the load are the major performance variables. For a fixed load, the system pressure directly affects the hydraulic gain. For example, a 10% drop in system pressure will cause a 5% decrease in actuator velocity. To make up for the drop in the hydraulic system gain, the controller must be able to open the valve 5% more. However, once the valve is fully open, the controller cannot compensate for the lower hydraulic system gain. When this occurs, either the requested speeds must be reduced or changes to the system must be made for the controller to maintain precise control.
One of the easiest ways to avoid a costly major redesign of the hydraulic system is to keep the supply pressure relatively constant by designing in more accumulators.
Accumulators as shock absorbers
In some applications, the hydraulic cylinders are stationary and some load tends to retract their piston rods. An example is rollers used for crushing rock. When a large rock enters the crusher, a roller must back off very quickly to relieve the mechanical strain. In these applications, the controller can do little to relieve the pressure because the valves cannot react quickly enough to relieve the pressure. Even a pressure relief valve may not react quickly enough to avoid jamming or causing damage to the system.
In this application, the amount of oil that must be relieved is usually just a matter of a few cubic inches. An effective technique is to place a small accumulator between the valve and the cylinder. Normally, this is not a good practice — especially with servo systems — because the accumulator increases compliance of the system. However, if the accumulator is precharged to a pressure above the system pressure then it will effectively be out of the circuit and have no effect on the motion control under normal conditions.
With these shock absorbing accumulators in place, when an object pushes the cylinder's piston rod back faster than the motion controller and valve are capable of responding, the pressure will increase above the system pressure and the shock absorbing accumulators will start to fill. The action of pushing back to cushion the shock will temporarily generate an error between actual and target actuator position, which will be reduced as the pressure returns to the normal system pressure when the obstruction passes or is removed and as the motion controller acts to reestablish the actuator position to match the target.
The hydraulic cylinders typically only need to retract a few inches in order to cushion a shock, so not much oil will be flowing into the accumulators. For example, a 3.25-in. bore cylinder that is pushed back 1 in. displaces only 8.3 in.3 of volume. Even if the accumulator size is only 1/2 gal, the pressure would increase by less than 8%. This is very effective shock absorption.
Accumulator sizing
Accumulator sizing programs are available from many sources on the web and from manufacturers for various accumulator designs. Generally accepted design requirements are that:
- the gas volume in the bladder should be large enough to prevent the pressure from dropping below a desired minimum level.
- the accumulator should never run out of oil.
This may seem obvious, yet few accumulators are actually charged such that these two goals are met. Usually, the accumulators have a too low a precharge (not enough gas), much more oil is in the accumulator than is ever used in one operating cycle. This results in the gas volume not being as large as possible. Because the energy storage capacity of the accumulator is proportional to the gas volume, the extra unused oil directly reduces the performance of the accumulator.
Sizing the accumulator accurately is a challenge, even when only one cylinder is involved. To begin, the designer must calculate the flow into and out of the accumulator as a function of time and determine the maximum change in volume from steady state. This requires knowledge of the motion profile of the actuator in order to calculate the amount of oil exiting the accumulator. The power unit pump flow as a function of the pressure should also be taken into account.
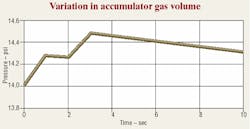
Figures 2 and 3 show how the supply pressure and gas volume change as a function of time in a low-duty-cycle example application. In this example, the supply pressure is 1500 psi. The cylinder extend motion occurs between 0 and 1 sec and the retract motion occurs between 2 and 3 sec. During the remaining time the accumulator is recharging to system pressure.
Notice that Figure 3 shows the recharging rate is reduced as the pressure builds back toward the system pressure. This happens when using a power unit with pressure-compensated pump as the pump's displacement control moves back toward its neutral position, and the error reduces between the actual pressure and the compensator pressure setting. These pumps react rather slowly to pressure changes.
An cylinder requiring quick acceleration will demand a high oil flow, making proper accumulator sizing critical. In such a system, the pump may take 100-200 msec to reach full flow — and then only after the pressure has dropped 150 to 200 psi, too late for the acceleration needs of the application. To be conservative in sizing the accumulators, it is best to estimate a generous change in gas volume. Systems using fixed-displacement pumps typically respond faster, so smaller accumulators can be used.
Calculations
Most designers use the ideal gas laws for their accumulator calculations. The ideal gas law,
PV= nRT,
can be stated simply as:
PV = K
Where:
P is pressure of the gas,
V is volume of the gas,
and K is a constant.
However, simple gas laws do not apply when there is little or no heat transferred into or out of the accumulators. Today's hydraulic systems move faster with higher cycle rates. Little time exists for heat to enter or leave the accumulator, so we should assume that the compression and expansion of gas is adiabatic — no heat is transferred into or out of the accumulator. Now the equation becomes more complex.
Where:
P1 is the supply pressure
P2 is the minimum pressure
V1 is the gas volume at steady state,
V2 is the total accumulator gas volume, and
γ is the ratio of specific heat, which is about 1.4 for diatomic gas.
Assume, as in Figure 2, that the system supply pressure is 1500 psi, and we wish to make sure the minimum pressure does not go below 90% (1350 psi). Referring to Figure 3, we see the amount by which the volume changes over time. As a good practice, we add a small safety factor. In the following example calculations — which apply to the similar system graphed in Figures 2 and 3 — one gal of capacity allows for the maximum amount of gas volume change plus the safety factor. This small safety factor ensures the accumulator will not run out of oil.
To calculate the gas volume required for the accumulator, we use the equation
Where
ΔV is the maximum change in gas volume plus a small safety factor. Solving for V1 yields:
This equation can be modified for V1 to obtain:
For this example we assumed the gas or oil volume changed by 1 gal and minimum pressure could not drop below 90% of the supply pressure. Because
13.8 gal is the total accumulator volume required.
In this case, we would use a 15-gal accumulator — the next larger standard size. Notice that the formula only uses the ratio of the pressures, not the absolute values. To limit the system pressure drop to 10%, we need a gas volume approximately 13 times the change in oil or gas volume. Also, note that calculations using the ideal gas law would suggest an accumulator size of 10 gal, which is significantly smaller and could lead to less than optimal motion control results.
Precharge pressure
Next, the precharge pressure must be calculated. The more difficult part is compensating for the change in temperature between the time the accumulator is charged and when the accumulator is operational. We assume this process will take time, so plenty of opportunity will exist for heat transfer between the oil and the gas. The equation we will use is the ideal gas law.
P V = n R T
The value of n is a constant, and T is temperature. However, this temperature is in degrees Rankin or, which is referenced to absolute zero, so roughly 460° must be added to °F.
The equation we will use is:
The 0 subscript indicates the precharge state, and the subscript 1 indicates the operational, steady state.
Assume the supply pressure is 1500 psi, the operating temperature, T1, is 120° F and the precharge temperature, T0, is 70° F. Now we can calculate the precharge pressure by solving the above equation for P0:
Replacing V1 with V0 - ΔV, and plugging in the numbers from above yields a pre charge pressure of:
P0 = 1279 psig.
Placing accumulators
Accumulators should be mounted as close as possible to where the energy is being used, not where it is being generated. This placement will reduce the pressure losses between the accumulator and the valve. Another consideration is that the flow between the pump and the accumulator is averaged out somewhat over a period of time. The peak flows will occur between the accumulator and the valve, so it is best to keep this distance short.
Even the most capable motion controller may not be able to compensate for a poorly designed hydraulic circuit, and the selection and location of accumulators is key to helping the motion controller do its work precisely.
Conclusions
Among the least understood system elements, accumulators have many purposes in hydraulic motion control applications. Three of the most important roles are storing energy, keeping the supply pressure constant and reducing shock. Storing energy allows for time averaging of the power demands resulting in reduced costs by using fewer and smaller pumps and motors. Keeping the supply pressure constant keeps the gain of the hydraulic system constant which makes the actuators easier to control. Finally, the ability to very effectively absorb shock protects both the hydraulics and the associated mechanical parts leading to longer machine life.
For more information, visit www.deltamotion.com or contact the author at [email protected].
This file type includes high resolution graphics and schematics when applicable.
About the Author
Peter Nachtwey
President,
Peter Nachtwey has more than 35 years of experience developing industrial control systems for hydraulic, electric, and pneumatic applications. He graduated from Oregon State University in 1975 with a BSEE and served as an officer in the U.S. Navy until 1980. He became president of Delta Computer Systems Inc. in 1992. In addition to leading Delta’s engineering and R&D programs, he contributes widely to the mathematical understanding of control theory, especially in fluid power systems. He has also presented technical papers for IFPE, NFPA, FPDA, and various global technical conferences.

Leaders relevant to this article: