Hydraulic-Electric Analogies: Capacitors and Accumulators, Part 1
This article is the latest in Jack Johnson's series on Hydaulic-Electric Analogies. See the "Related" articles list below for previous articles in the series.
This file type includes high resolution graphics and schematics when applicable.
Electrostatic fields are relatively unimportant in the hydraulic world, but they have great significance in the electrical and electronic media. From an electrohydraulic point of view, the most important use for the electrostatic field is in the electrical capacitor. Analogously, the electrical capacitor is significant in that it gives rise to the hydraulic capacitor.
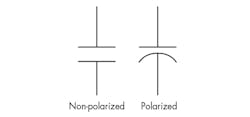
Not surprisingly, electrical capacitors are rated in terms of their capacitance. Capacitors can be either polarized or non-polarized (Fig. 15). Polarized types require that applied voltage polarity be strictly observed, while non-polarized caps don’t have that constraint.
The working units for capacitance are ampere-second/volt, otherwise referred to as farad. The popular workaday unit for capacitance is the microfarad, a millionth of a farad, normally abbreviated as µF. Again, as in the case of inductors, time enters into the units and interpretation. Hydraulic capacitance in conventional US units would be (in.3/sec) sec/psi, which can be simplified to in.3/psi. That can be further simplified to in.5/lb when measuring flow in the very convenient in.3/sec and pressure in psi.
Hydraulic capacitance has no established workaday unit. However, I unabashedly refer to the hydraulic farad and hydraulic microfarad, and abbreviate them as hyfd and the µhyfd, respectively. In the metric world, the working units for hydraulic capacitance are the unwieldy lpm × sec/bar when pressure is in bar and flow is in liters per minute. As of this point, no known movement has emerged to standardize this anomalous construct.
An electrical capacitance exists any time two conductors are separated by a dielectric. For the moment, a dielectric material is an insulator; that is, some material that does not conduct electrical current. There are two kinds of electrical capacitance: deliberate (which is not an accepted technical term) and unintentional, better known as parasitic capacitance.
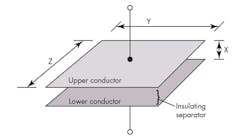
The deliberate capacitor, a device that’s been built, sold, and applied for its special electrical properties, is deliberately wired into the receiving circuit (Fig. 16). Capacitance is directly proportional to the area of the plates (Z×Y from the figure) and inversely proportional to the plate separation, x:
C = ε × A/x
where C is capacitance; ε is the permittivity of the material (a property of the dielectric separator); A is the area of one of the plates in the simple parallel plate construction; and x is the plate separation distance.
Free space has a permittivity of 8.85 × 10-12 farad/m. Some glass has a permittivity that’s 10 times higher, and strontium titanate is 200 times greater. Capacitor designers take advantage of the permittivity values to get higher and higher amounts of capacitance in ever-decreasing package sizes.
The parasitic capacitance doesn’t arise through deliberate human processes, but rather because the circuit is built using conductors. And all conductors are separated from other conductors by insulators, preventing the potentially tragic consequences of having the currents in one conductor leak into the conductors of other circuits.
In other words, if you build a circuit, it will have parasitic capacitances. The aim is to keep their values low enough so that the capacitive properties don’t appreciably affect the circuit’s performance. Fortunately, the affects of parasitic capacitance in, for example, a typical servo amplifier, or proportional valve amplifier, are negligibly small.
The Deliberate Electrical Capacitor
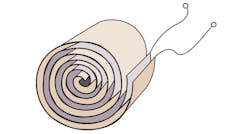
Capacitance increases by expanding the area of the conductor. Two parallel plates will exhibit measurable capacitance, which can be enhanced by placing the plates closer together. In the construction of the capacitor, the plates are separated by a thin insulating material measuring only a few thousandths of an inch thick. Figure 17 shows how the two conductors are rolled up in a spiral manner to stuff the two-layer assembly into a small cylindrical can. The two conducting layers are separated by two respective layers of the insulating materials (not shown in the figure). This construction method produces the greatest possible capacitance in the smallest possible volume.
Before exploring deeper into how the electrical capacitor works, let’s first discuss the hydraulic capacitor to gain physical insight. The key factor here is that the electrical capacitor stores charges (electrons and those other fictitious positive things), while the hydraulic capacitor — the accumulator — stores molecules of hydraulic fluid.
The Deliberate Hydraulic Capacitor
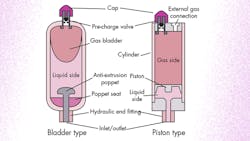
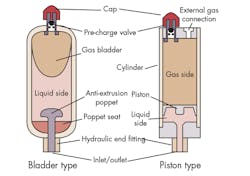
Similar to the electric capacitor, capacitance in the hydraulic circuit is both deliberate and parasitic. The deliberate hydraulic capacitor, called an accumulator, can be constructed in any one of several ways. The most common construction is gas-over-liquid, which incorporates either a bladder or piston (left and right, respectively, Fig. 18) to separate the compressible gas chamber from the liquid chamber.
It’s generally accepted that the two accumulators have essentially identical characteristics; however, research is needed in terms of comparing their performance. Like so many mechanical and hydromechanical machines, having some knowledge of their construction aids in understanding their function. The two accumulator types in Figure 18 offer a good starting point.
In the accumulator symbol (Fig. 19), there’s only the essential parts—the hydraulic inlet/outlet port, the liquid side, the gas side, and the separator. The open triangle on the gas side conveys that it’s precharged with a gas, but doesn’t indicate the type of gas nor the amount of precharge on the gas side. The symbol also doesn’t reveal the construction type. The colors are non-standard.
Regardless of the construction type, the practical hydraulic capacitor has a gas side and a liquid side. The liquid side (hydraulic side) is typically connected to the active hydraulic circuit in its application. The gas side is usually “pumped up” to some precharge pressure with an inert gas, such as argon or nitrogen. The precharge pressure is in the same range as the operational pressure in the hydraulic system, which is in the hundreds or thousands of psi. Inert gases are used to avoid the possible combustion of hydraulic fluids that may inadvertently come into contact with the pressurized gas. Oxygen-containing precharge gases could support the combustion.
Proper and normal operation of the accumulator requires isolation of the liquid and gas sides from each other. When the accumulator is “sitting on the shelf” with some gas precharge pressure, the hydraulic port will be at atmospheric conditions. As a result, the precharged gas forces the bladder to completely fill the interior of the accumulator. In so doing, the bladder will contact the anti-extrusion poppet, which closes the poppet and prevents the bladder from extruding out of the hydraulic inlet/outlet port. Likewise, the gas will force the piston of the second type into its bottom position and fill the gas side.
How it Works
When connecting the accumulator into a functioning hydraulic system, realize that the accumulator will not be active until the hydraulic pressure reaches and exceeds the gas precharge pressure. After exceeding the precharge pressure on the hydraulic side, hydraulic fluid can enter and exit its side of the inlet/outlet port. As the liquid enters and exits through the hydraulic port, the gas is alternately compressed and decompressed.
In addition, energy is stored in the compressed gas. This energy storage capability allows the accumulator to quickly release energy and liquid volume in the event that the hydraulic circuit has a sudden demand for flow. In fact, this is one of the most important functions of accumulators.
The performance of a gas-over-oil accumulator is governed by gas laws. However, gas laws are limited in two instances: adiabatic and isothermal operation. In adiabatic operation, no thermal energy caused by the gas compression leaves the system. In isothermal operation, all energy of gas compression leaves the system so that the gas operates at a fixed temperature.
Between the two modes, adiabatic operation is the most likely to appear in hydraulic systems. This requires that one, or both, of the following events take place. First, the cycling of the system pressure and the concomitant instantaneous gas temperature changes occur so quickly that thermal energy has no chance to leave the interior of the accumulator. Or, the accumulator must be effectively insulated to impede heat transfer.
Accumulators usually aren’t insulated. However, because most industrial processes cycle quickly enough, it’s reasonable to assume that they’re in adiabatic mode. Isothermal operation is interesting, but it won’t likely be found in hydraulic systems due to the time required to transfer heat energy through the accumulator’s walls to keep gas at some fixed temperature.
Formulas for Gas-Charged Accumulators
Figure 20 shows an approximate graph of a hydraulic accumulator’s adiabatic operation. VO represents the hydraulic volume of liquid (usually oil) that enters the hydraulic port of the gas-filled accumulator. PPC is the gas precharge pressure value. Note that no volume enters the liquid side until the hydraulic pressure (PS) reaches and exceeds PPC.
Further increases in hydraulic pressure result in greater amounts of hydraulic fluid entering the accumulator. When the hydraulic pressure decreases, hydraulic fluid leaves the accumulator. In other words, fluid will flow through the hydraulic throat only when the hydraulic pressure is changing and when it exceeds the gas precharge pressure. When pressure is constant, there’s no hydraulic flow going into or out of the accumulator.
Starting with the ideal gas laws, the volume of oil resulting from the hydraulic inlet pressure is:
VO = VACC [1 – (PPC/PS)1/n]
where VO is the volume of fluid ingested into the accumulator to raise the pressure from PPC to PS; VACC is the actual physical volume of the accumulator; PPC is the absolute precharge pressure of the accumulator; PS is the absolute inlet hydraulic pressure; and n is the dimensionless universal gas constant that depends on the precharge gas. For example, nitrogen’s constant is generally accepted as 1.4, whereas argon is about 1.67.
It’s important to use absolute pressures in the equation, so just add about 15 psi (1 bar) to the gauge pressure values when doing the calculations. The assumption of an ideal gas is reasonable at pressures encountered in most hydraulic systems.
Hydraulic capacitance is the slope of volume-pressure curve under a given operating condition. The adiabatic capacitance for the precharged accumulator is:
CH = (PPC1/N × VACC) / (n × PS[n-1]/n)
where CH is the hydraulic capacitance (measured as in.5/lb in IPS units). Other terms in this equation were defined earlier in the article.
This file type includes high resolution graphics and schematics when applicable.
Three distinct advantages emerge when using a parameter like hydraulic capacitance. First, it allows the comparison of the deliberate capacitance to the parasitic values, enabling the elimination of parasitic capacitances when they’re obscurely small. Second, all of the circuit theorems developed and used by electrical engineers through the decades thus becomes easy to apply to hydraulic circuits. Third, using familiar elements and equations means that electrical engineers are more likely to become interested in hydraulic-circuit analysis if their starting point has familiar terms and concepts.