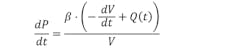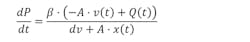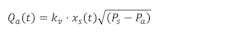Controlling pressure is key to motion and force control, but there is little understanding of how pressure is controlled. A common misconception is that pressure is “resistance to flow,” or that pressure is controlled by servo valves using the pressure gain curves. It is time to take a closer look at exactly what happens when a hydraulic system operates.
One of the basic formulas for pressure change is:
Where ΔP is the pressure change, Β is oil’s bulk modulus, ΔV is the change in volume under pressure and V is the total volume under pressure.
So, if the volume under compression decreases, the pressure will increase. This is what happens when a cylinder rod is impacted and the oil on the cap side of the piston is compressed.
The formula above is useful in relatively static situations but in dynamic situations, such as motion or force control, the formula must be modified to include time. Now the formula becomes
or
Where dP/dt is the instantaneous change in pressure and dV/dt is the instantaneous change in the compressed volume of oil.
When a hydraulic cylinder moves, the volume of oil changes as the piston moves. To keep the pressure constant, dP/dt must equal 0. Therefore, oil must be added or subtracted from the cylinder. The formula for dP/dt must be expanded to include flow.
Notice that increasing the volume makes the change in pressure negative. But if the flow as a function of time, Q(t), equals the rate of change in volume under pressure, pressure remains constant.
Next, the volume and change in volume needs to be expanded. The change in volume of oil equals the area of the piston times the velocity of the piston. The volume of oil under compression equals the dead volume plus the distance from the piston to the end of the cylinder. The resulting equation is
Where A is the area of the piston on the cap side in this example, dv is the dead volume of oil between the fully retracted piston and valve, x(t) is the piston position relative to the fully retracted position, and v(t) is the piston velocity as a function of time. It is positive when they cylinder moves away from the fully retracted position. When v(t) is positive, pressure in the cap side of the piston drops unless oil is added.
The piston position and velocity can be measured using a feedback device, which is typically a magnetostrictive transducer rod. The flow is not measured but, rather, is controlled indirectly by a hydraulic motion controller directing a proportional valve. When modeling or simulating, flow can be estimated closely using the manufacturer’s specification. First calculate the valve’s flow constant using:
Now the flow can be calculated as a function of the pressure and the spool position x(t) using:
The spool’s position is controlled by the motion controller’s output. Ps is the supply pressure and Pa is the pressure in the cap side of the cylinder. Notice that the pressure change in the cap side of the cylinder depends on many factors, including the pressure in the cap side of the cylinder! This requires a sophisticated calculation.
Sometimes pressure only needs to be controlled, as when testing a container’s ability to withstand pressure. In such cases, only a sensor monitoring pressure inside the container is needed.
Usually, the pressure is used to control the force applied to an object. In this case, the pressure on each side of the piston is multiplied by the area of the corresponding piston and the difference is the net force. In this case, the motion controller is closing the loop around the net force. To calculate the net force requires a load cell or pressure sensor mounted so it can measure pressure on each side of the piston.
During motion control, the pressure is also controlled indirectly. However, when simulating net force and motion, there must be a set of equations for each side of the piston because the net force is required. The net force is used to calculate acceleration. Acceleration is then integrated to determine the velocity, and then velocity is integrated to determine position.
Obviously, the equations for calculating pressure changes are complicated and depend on many factors that are constantly changing. Hydraulic simulators use the current state to calculate the next state in small time increments. Usually increments of 100 microseconds are sufficient. The reason for using small time increments is that pressure changes quickly when an obstruction is hit, as in a press. Plus, the smaller the time increments, the better and smoother the simulation will likely be. The tradeoff is the additional calculation time needed and the large amount of data generated.
Back in the early 2000s, I used a spreadsheet to simulate a customers’ system which had been designed incorrectly. At that time, my spreadsheet program could only handle 32,768 rows. But at 100 microseconds for each row, I could only simulate 3.2 sec., which fortunately was long enough.
Each column was an equation for calculating position, velocity, acceleration, net force, cap side and rod side pressure. Once the first row was complete, the formulas were copied to the rest of the rows. Pressure changes depend on these values, so they had to be calculated for each row or in 100 microsecond iterations. It worked but was limited by the speed and memory capacity of personal computers back then.
The next article will show how calculating pressure changes is like calculating interest on savings; calculating interest compounded daily is also an iterative process.
Peter Nachtwey is president of Delta Computer Systems, Battle Ground, Wash. For more information, call (360) 254-8688, or visit www.deltamotion.com.
