Closed-loop speed control of hydraulic motors
We must know the load torque in an application to correctly predict the speed gain of the system. Because loads can be quite complex, load torque rarely is constant. Therefore, we usually have to settle for an approximation or analyze extremes of zero load and maximum load.
The electrical control input signal modulates the valve coefficient, and the electrical drive for the valve is always supplied by an amplifier. Furthermore, the gain is adjustable, so the user assembles the speed control loop, then carefully increases the electronic gain until the desired performance is achieved. In most cases, the user never even knows the actual speed gain at application time!
If the valve's flow metering characteristics are reasonably linear, then a linear relationship exists between electronic control input and the valve coefficient. Therefore, under these conditions, motor speed is a linear function of the command signal. However, this discussion applies to an open-loop system, but we are interested in closed-loop performance.
Closing the loop
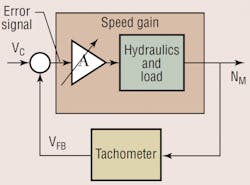
Closed-loop control is easily accommodated, too. An analog amplifier subtracts the feedback signal from the command signal to yield an error signal. With no feedback, the command signal is also the error signal. In a digital control system, the error is generated from a simple calculation. In either case, when the feedback is connected to the servo or proportional amplifier's feedback input terminal, the system can be depicted as shown in Figure 1. The electronic amplifier, A, is shown as being adjustable, so that the overall gain (in this case, the rpm/V of error signal) can be set to any arbitrarily high or low value.
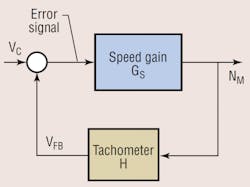
The block diagram in Figure 1 can be simplified by combining the elements in the speed gain block and lumping them altogether into an algebraic variable called GS. The result is shown in Figure 2. The universal language of block diagraming and control system design uses the symbol H to indicate the feedback path. In this case it consists solely of the tachometer, whose output is the feedback voltage, VFB.
Establishing relationships
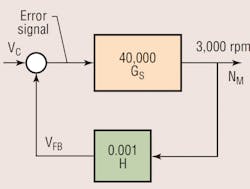
As we concluded in a previous edition, the error voltage cannot be zero when the control loop settles out. Assume, as before, that the tachometer constant, H, is 1 V/ 1000 rpm. We also need to know the speed gain, GS. A realistic value might be, say, 40,000 rpm/V.
Figure 2 can be redrawn with numerical values in the blocks, Figure 3. Let us now assume that the output speed is 3000 rpm. With output at 3000 rpm, and a speed gain of 40,000, the error voltage is 3000 divided by 40,000, or 0.075 V. Also, with 3000-rpm output, the tachometer output voltage must be 3.000 V. Thus, the command input voltage must be 0.075 V greater than the feed back, or 3.075 V for the command minus the feedback to agree with the error voltage value. The system is in equilibrium, and the error is not zero! Two principles are at work here. First, it should be clear that the larger the speed gain, the lower the error voltage. Second, just because a controlled variable is feedback to the system input, that variable is not necessarily perfectly regulated. In addition, even though the command input is constant, any changes in speed gain caused by any parameters within it — such as supply pressure, load torque, or motor displacement — will result in a change in output speed.
Rather than the simple proportional controller discussed to this point, an integrating controller is required to overcome the steady-state error problem in the speed control loop. Such controllers are generically called PID controllers. The variation shown in Figure 4 is a PI controller, that is, the derivative function is missing. It is commonly used in electrohydraulics because experience has found this to be all that is needed.
The proportional function in Figure 4 is symbolized by the bold numeral 1, indicating that it has a gain of one, which makes calculations much easier. In fact, the proportional gain normally is adjustable on commercial controllers. Note that the proportional element and the integrator (symbolized by an integral sign) share a common input, namely the error signal, . The two outputs are added together, and their sum forms the input into the speed gain block.
The function of integral control and its variations is to reduce the steady-state error to zero. In that serendipitous condition, the command and feedback are equal. If we want a speed of, say, 1520 rpm, and the tachometer is 0.001 V/rpm, then the command signal should be set to 1.520 V. Predicting the output based on command is much easier with integral control.
This begs the question, "How does the addition of an integrator reduce the steady-state error to zero?" The error is necessary in the simple proportional case because the valve must be open for the motor to turn at some speed. The error is the only voltage available in the simple proportional case, so the command and feedback must be non-zero.
Now consider the integrator, involves infinite summation or accumulation. The characteristics of a physical integrator — like the one in the controller above — are such that if an input signal is not zero, the output is changing. When the input is zero, the output remains at its last, or accumulated value. We say that it is integrating its input — the error signal in this case.
Idealized integrator
Keeping the integrator characteristic in mind, we'll revisit the operation of the system to see what is happening in the controller and to the output speed. With the controller of Figure 4, suppose our input command of 3.075 V is suddenly applied while the motor is stopped. The motor will quickly accelerate to about 3000 rpm, at which time the error will be 0.075 V. That will keep the valve open while a new equilibrium point is reached.
Now the integrator starts to take over. Because its input is not zero, its output will begin to grow. Suppose it grows to, say, 0.030 V. That is added to the proportional output, which has grown to 3.040 V. Therefore, the speed rises to 3040 rpm, producing a feedback voltage of 3.040 V, which produces an error signal of 0.035 V (3.075 - 3.040). But the error is not zero, so the integrator's output grows more. Let's say it grows to 0.070 V. Now the speed rises to 3070 rpm, the feedback is 3.070 V, and error is now 0.005 V — still not zero. However, the trend is established.
The integrator output will no longer grow only when the error reaches zero. This condition requires a feedback voltage of 3.075 V and an output speed of 3075 rpm. If we now reduce the command to 3.000 V, we can reasonably expect the output speed to be 3000 rpm and the error to be zero.
This discussion is quite idealized, and all real servo loops have some error. Therefore, the speed will not be exactly 3000 rpm, and it will not be perfectly constant because of the noise that is inherent in any control system. However, it will be closer than with proportional control only. Instability of the control loop is also a possibility.
Important considerations
Integral control in speed loops is quite common because of the otherwise steady-state error problem. Plus, integral control carries a performance cost.
First, consider that it takes some time for the integrator to do its integration thing. This means some loss in responsiveness occurs. I have worked out the increase in time to reach steady-state for a positional servo to be about 33% longer after adding integral control. More research needs to be done on the speed control loop. However, a settling time penalty of 33% is probably a reasonable guess without further information. This means that if a speed loop is constructed with proportional control only, and it will settle to steady-state in, say, 360 msec, then settling time can be expected to increase to about 480 msec after adding the PI controller.
Second, consider that the speed of response is directly related to the integral gain. The higher the gain, the more quickly the integrator will charge, and the more quickly the loop will settle. Trying to speed up the loop with higher integral gain will quickly lead to system instability — continuous hunting for the quiescent point and never settling out.
Integral control invariably creates a system with more stability problems than with simple proportional control. Even in when the system is tuned for stable operation, a springy operation can be expected wherein the output speed overshoots the steady-sate target, but it eventually settles.